Chapter 6: Where are we going?
Let's play the ancient game of Nim. We have a pile of seventeen pebbles. We will take turns removing either one, two, or three stones from the pile. Whoever is left with the last pebble loses the game.
Can you imagine how to program such a game? If your answer is "yes," then perhaps you should stop reading and try it! If your answer is "maybe," then keep reading. So far, the game of Nim is just an idea. That is how all programs start out. This chapter is about turning ideas into programs.
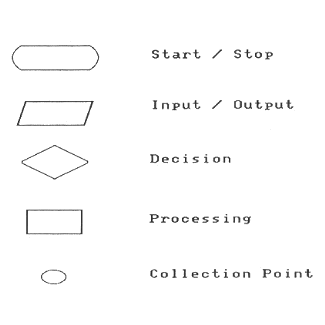
As our programs become longer and more complicated, it becomes more difficult to easily see what they do and exactly how they work. One tool to help us understand programs is a FLOWCHART. A flowchart is a special kind of diagram showing the order in which things happen in the program (that is, the flow), along with the decisions (IF-THEN statements) that might change the flow. Five symbols are used to describe all actions. (See Figure 1 on page 63.) Each one describes a certain type. They are: start/stop, decision, input/output, and process. Lines with arrows connect the boxes to show program flow. Each symbol contains a short description of the function represented by the box.
Ovals mark the beginning and end of the program. The beginning oval should have the word "Start" in it. The ending oval will contain "Stop."
A diamond represents decisions. A decision box has one line entering it and two lines leaving. The two lines map the two possible outcomes of an IF-THEN test. For example, if we have the statement:
840 IF CHOICE% = 2 THEN GOTO 1500 ELSE GOTO 1800
the diamond decision block should contain "Does CHOICE% = 2?." One point of the diamond will be labeled "yes" with a line connected to the symbol describing the processing at line 1500. Another point of the diamond, labeled "no" connects to the symbol representing line 1800. In this case we have mapped a single line of the program to a flowchart symbol. This is not always the case. Flowcharts summarize the processing. If a symbol was used for every statement the flowchart would be as confusing as the program.
Decisions are so important that they usually deserve the special attention.
Input and output (I/O) are represented by parallelograms. To use, draw the symbol and write a few words about what I/O operations are taking place. An example might be "print menu" or "input answer."
A rectangle is used to describe processing that does not involve decision-making or I/O. For example, the UGUESS program from the last chapter could have used one labeled "get a random number in the range 1 to 100."
The last symbol that we will use is just a small simple circle. The circle is called a COLLECTION POINT and is used to connect two or more lines.
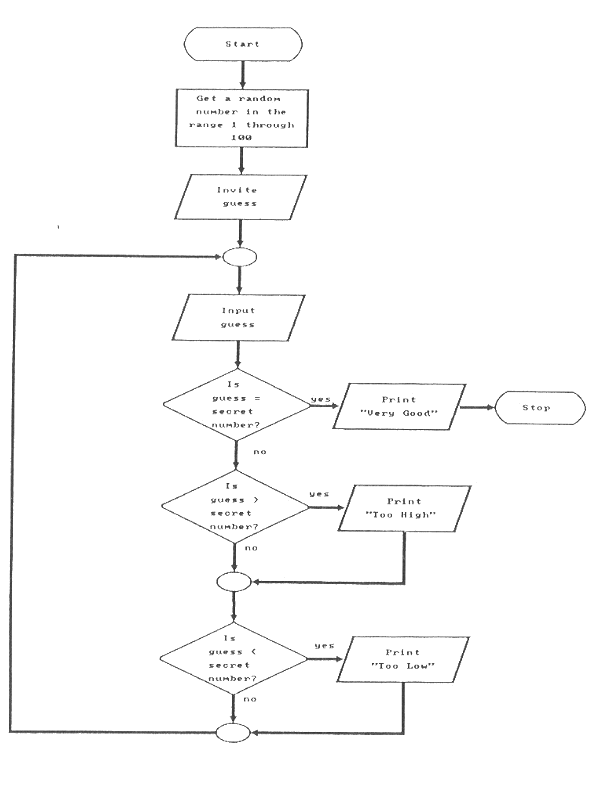
Let's see these symbols in action. Examine Figure 2 on page 65. This is a complete flowchart of the program. Processing begins with the start oval. First, a rectangular processing box obtains a random number. Then, execution moves down to the input/output box. Compare this flowchart with the program listing. The "invite guess" I/O box clears the screen and then asks the player to guess the number selected by the program. Their response is symbolized by another I/O box labeled "input guess."
Then we reach the first decision box. The first question is whether the guess is correct. If yes, execution moves to the I/O box labeled "print 'very good'" and the program ends. If the guess is not correct, we move down the line labeled "no" out of the first decision box into the second. This decision box tests if the guess is higher than the secret number. If yes, then the "too high" message is printed. If no, then the next decision box is reached. Notice that this second decision box is executed even if the greater than test is true. After printing the "too high" message, the line continues to a connection point just ahead of the less than test.
After the last decision box, execution is returned to the "input guess" I/O box higher up the chart. With this flowchart it is clear to see that the only way out of the loop is to guess the secret number and pass the test at the first decision box.
Flowcharts are good, not only for programs, but also to explain any complicated process. For example, you could flowchart getting up in the morning and everything that must happen to get out of the door on time. Such a chart would have plenty of decision boxes labeled "am I late?"
Programming flowcharts are valuable in several ways. First, they explain what happens in a program. This is what we have just done with the UGUESS1 program. The program came before the flowchart. Now we can see in one simple picture all the tasks performed by the program. The chart is useful if we need to explain our program to someone not familiar with BASIC. More importantly, flowcharts are useful when we plan new programs. As you begin to think about a program, it is helpful to draw flowcharts. They do not need to be elaborate, carefully drawn works of art. A chart is just a tool.
If you understand a process well enough to do a flowchart, you probably understand it well enough to write a program. Flowcharting helps you think through a problem. You do not need to flowchart every step of a procedure. Use the rectangular process blocks to cover entire subroutines. Indeed, for larger programs, you will almost certainly start this way. Begin by drawing a flowchart that shows the major steps, the order in which the subroutines are called, for instance. Later, other flowcharts can be drawn which detail exactly what happens in each routine. Usually, you will find that working out the details in the subroutines causes you to change the original chart. That is okay. It is better to find out about changes while working on a flowchart than it is to make this discovery after writing dozens of lines of BASIC code.
THE GAME OF NIM
With flowcharts in our tool bag, it is now time to build a program to play the game of Nim. Here is what the program must do:
- Set a variable named QUANT% to 17. These are the pebbles.
- Decide who goes first, the human or the computer. Put the result in a variable called WHO$.
- Let the computer randomly pick 1, 2, or 3.
- Make sure that subtracting the computer's random number from QUANT% does not leave a number less than one.
- Ask the human to subtract 1, 2, or 3.
- Make sure the human does not cheat in any way.
- When only one pebble is left (QUANT% = 1) print a message.
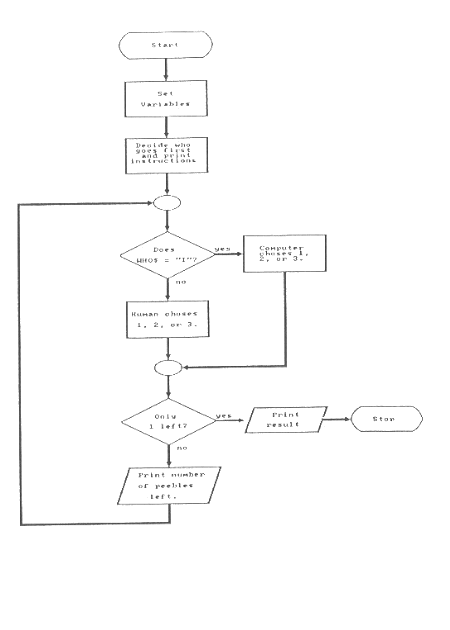
These are our program specifications. This is not yet enough information to start writing. Instead, let's flowchart the main tasks. Refer to Figure 3 on page 67. The first process box defines the variable QUANT%. Next, we have a process box labeled "print instructions and decide who goes first." We can place all of these tasks in a subroutine. Obviously, the subroutine will have its own I/O and decision boxes. It may be a complicated subroutine. We will worry about it later. Right now, we can assume that somehow we will figure out how to decide who goes first.
Next in the mainline routine is a test. This one will use the result of the previous process box. Now our program needs to know who really is taking the first turn. This is known by checking a string variable names WHO$. If WHO$ is equal to "You" then the human takes a turn. If WHO$ is "I," the computer gets a turn.
The decision box leads to two process boxes. In one, the computer somehow choses 1, 2, or 3. In the other, the human enters a number to subtract. These subroutines will also prevent the human from cheating and the computer from subtracting 3 from 2. Remember, computers are dumb. Each subroutine will also switch WHO$. The computer process box changes WHO$ to "You" so the human can have a turn next time through the loop.
Finally, a decision box checks to see if only one pebble is left. If it is, a nice message is printed. If more than one remain, print the number remaining and go back to the start of the loop.
This looks like it will work. We can see already that the first decision box is very important. If the computer and the human are to take turns, then the WHO$ variable must be switched every time a turn is taken. Think of WHO$ as a sign hanging on a wall. It tells who is supposed to take a turn. After you take your turn, you flip the sign so the other play knows to take a turn. Also, WHO$ will be used to know who lost the game.
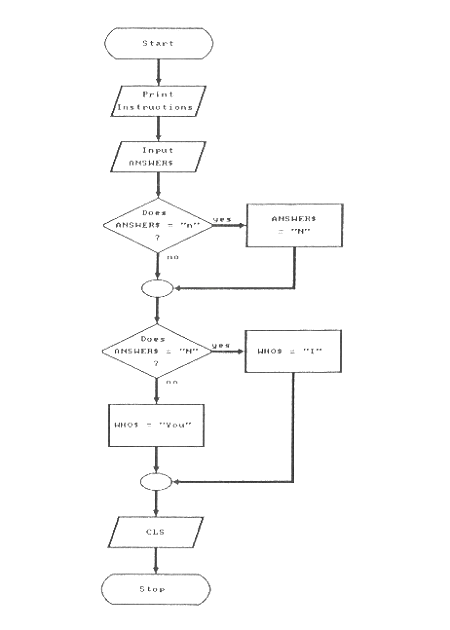
Now let's tackle the first subroutine. See Figure 4 on page 69. One way to decide who goes first is just to ask the human player to chose. The subroutine asks "Do you want to go first?" The answer can be either "yes" or "no." Since we write user friendly programs, we will only require that they enter the first letter of their answer. Indeed, our program will only test for a first character of "n." The first decision box checks for a lower case "n." If one is found, then it is changed to an capital "N." The next decision box checks to see if the first character of their answer is a capital "N." If yes, then the human does not want to go first and WHO$ is set to "I" (meaning the computer). If the human wants to take the first turn, then they must enter anything that does not begin with either an upper or lower case "N." The second decision box comes out false and WHO$ is set to "You."
Finally, the subroutine clears the screen and returns to the mainline routine.
The main purpose of this subroutine is to set WHO$ to either "I" or "You." The routine also prints the instructions on how to play Nim, but this is secondary. We could easily divide the two tasks into separate subroutines, one to print instructions and another to decide who goes first. Can you think of any other way to decide who goes first? Perhaps we could toss a coin. Instead of asking the player to decide, we could create a random number in the range of 1 to 10, and then test if it is less than 5. If yes, then the computer could go first. Half the time, the human should win the toss. Since we make this choice in a subroutine, we might wish to try out several other ways. We could even get a random number between 1 and 100 and ask the human to guess if it were greater than or less than fifty!
Learn to think in terms of subroutines, the basic building blocks of programs. The mainline routine is the design of our program. The subroutines must contribute certain things to the mainline, in this case, the variable WHO$. You may even write and test the subroutines before the mainline.
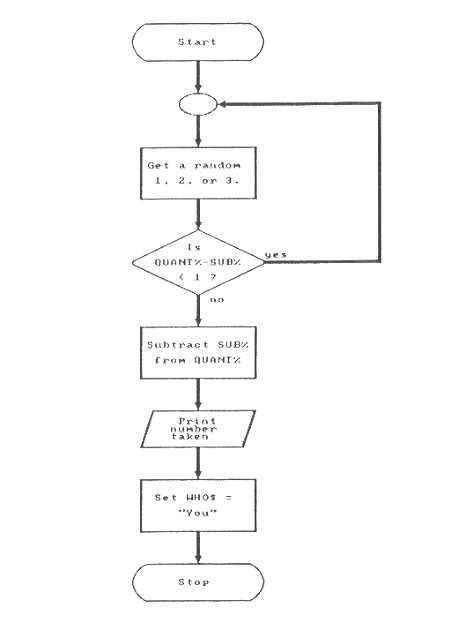
The process box labeled "computer choses 1, 2, or 3" is simple. It has only one decision box. Look at Figure 5 on page 70. This one begins with a process box that selects a random number in the range 1 to 3. Since computers are dumb, it may chose to subtract three when only two pebbles are left. Therefore, we have a decision box that catches this. If necessary, another random number is selected. Only when a correct choice is made will the subroutine continue. It performs the subtraction, prints the number subtracted, sets WHO$ to "You," and returns to the mainline routine.
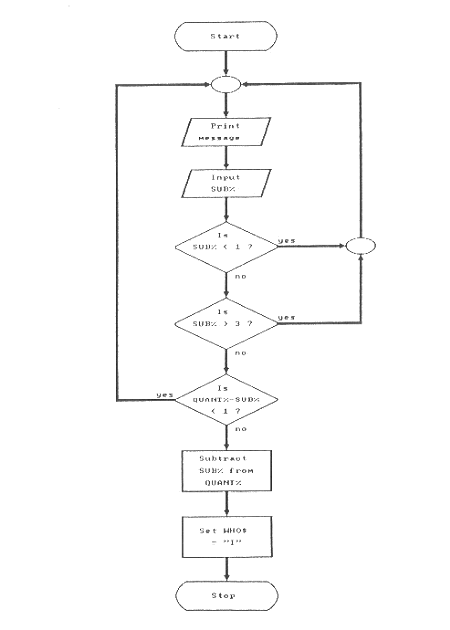
By way of contrast, the subroutine which allows the human to take a turn is far more complicated. See Figure 6 on page 71. This part of the program is complicated because humans cannot be trusted. The player may decide to go first and
subtract 16! Or if the human gets in a tight spot, they may subtract zero! We can't let that happen. Therefore, after we print a message inviting the player to subtract 1, 2, or 3, we accept their input and then performs three tests. The first checks to see if the number entered is less than 1. If yes, then force the person to pick another number. The second decision box tests to see if the number entered is greater than 3. These two tests weed out the big cheats. Finally, we perform the same test as we did when the computer was chosing a number. Only when all three tests are passed successfully will the number be subtracted from the QUANT% variable. Finally, WHO$ is set to "I" and the subroutine returns to the mainline program.
At least on paper, we have solved all of the problems needed to create a new computer game. Now we must turn these flowcharts into lines of BASIC. We will start with the subroutines.
NIM1 uses four variables. WHO$ is a string variable which controls taking turns. ANSWER$ is a string variable used in the first subroutine. It is only used to set up WHO$. QUANT% is the number of pebbles. It starts out at 17. SUB% is another integer variable. This is the amount that is subtracted from QUANT% each time a player takes a turn.
The first subroutine prints the instructions to the game and decides who goes first. The output of this routine is WHO$.
800 CLS 810 PRINT "****************************************************" 820 PRINT "* *" 830 PRINT "* Test your skill at the ancient game of NIM ! *" 840 PRINT "* *" 850 PRINT "* We will start out with 17 objects. You will take " 860 PRINT "* turns with the computer and you may take away 1, 2, 870 PRINT "* or 3 of the items. The object of the game is to *" 880 PRINT "* avoid getting stuck with the last item. *" 890 PRINT "* *" 900 PRINT "****************************************************" 910 PRINT "Do you want to go first? Enter Yes or No." 920 INPUT ANSWER$ 930 IF LEFT$(ANSWER$,1) = "n" THEN ANSWER$ = "N" 940 IF LEFT$(ANSWER$,1) = "N" THEN WHO$ = "I" ELSE WHO$ = "You" 950 CLS 960 RETURN
Line 930 introduces a new BASIC function. LEFT$ returns the leftmost characters of a string variable. Here is the syntax:
LEFT$(variable,number-of-characters)
The parentheses contain the name of the string variable along with the number of characters needed. Line 930, for example, gives us the one leftmost character in the variable ANSWER$. If we wanted two characters, we would write:
930 IF LEFT$(ANSWER$,2) = "no" then ANSWER$ = "NO"
To explore the LEFT$ function some more, enter this program:
10 WHO$ = "Jabberwocky" 20 FOR X% = 1 TO 11 30 PRINT LEFT$(WHO$,X%) 40 NEXT X% 50 END
LEFT$ allows us to be user friendly. Remember our discussion of string variables in chapter one. NO, no, No, and nO are all different to BASIC. We need a way to recognize what the person means. The best way is to look at just the first character of their answer. Line 930 checks to see if the first character is a lower case "n." If it is, then it is converted to an upper case "N." Line 940 tests for a capital "N." ANSWER$ may contain an upper case "N" either because that is the first letter of the word "No," or because line 930 set it to "N." Line 940 then decides what letters will be placed in the WHO$ variable. Once WHO$ is defined, our subroutine has done its job. So we can clear the screen and return to the mainline program.
The next subroutine permits the computer to subtract a number. Compare these BASIC instructions with Figure 5 on page 70.
300 REM *** The computer will randomly take 1, 2, or 3. * 310 RANDOMIZE TIMER 320 SUB% = INT(1 + RND * 3) 330 IF QUANT% - SUB% < 1 THEN GOTO 310 340 QUANT% = QUANT% - SUB% 350 PRINT "I have subtracted " SUB% 360 WHO$ = "You" 370 RETURN
There should be no surprises here. The RANDOMIZE TIMER statement only needs to be executed once in a program. By placing it in this routine, it gets executed every time the computer takes a turn. No harm is done. It was placed here because this is the routine where a random number was needed. Thus, all the statements having to do with random numbers were kept together in one place.
Line 320 is a standard formula for randomly getting a 1, 2, or 3. The random number is placed in the integer variable SUB%. The next line matches the decision box on the flowchart. If subtracting SUB% from QUANT% would leave us with a number less than 1, then we must select another random number. When only three pebbles are left, the computer may subtract one or two. Line 330 will not let it subtract three.
Since the computer cannot cheat, we do not have to perform as many tests as we will for the human player.
Line 340 finally performs the real subtraction. Then we print a message. Finally, line 360 changes WHO$ so the human player gets to take the next turn.
The last major subroutine turns control over to the human player, that most untrustworthy beast. The BASIC statements exactly match the flowchart in Figure 6 on page 71.
500 REM ***** The human can take a turn ***** 510 INPUT "Please subtract 1, 2, or 3. ",SUB% 520 IF SUB% < 1 THEN GOTO 500 530 IF SUB% > 3 THEN GOTO 500 540 IF QUANT% - SUB% < 1 THEN GOTO 500 550 QUANT% = QUANT% - SUB% 560 WHO$ = "I" 570 RETURN
Hopefully, a line-by-line description is not needed -- with one exception. Look closely at line 510. This looks like we mixed a PRINT command with an INPUT statement. And that is exactly what we have done! Since an INPUT statement almost always requires a PRINT in front of it, BASIC allows us to include a short message to display on the screen. When line 510 is executed, BASIC displays all the characters included within the quotation marks, just like PRINT, and then waits for keyboard input to set the integer variable SUB%. Line 510 is a short way of writing:
510 PRINT "Please subtract 1, 2, or 3." 515 INPUT SUB%
Compare each line of BASIC with the flowchart. Both the flowchart symbols and the BASIC statements should be comfortably familiar by now.
Before we write the mainline routine, one more subroutine is needed. When only one pebble is left, we must stop the game and say who lost.
1000 REM ***** THE END OF THE GAME ***** 1010 PRINT "Only 1 is left. " WHO$ " lose!" 1020 END
Notice how line 1010 works. WHO$ points to the player (either "You" or "I") who is to take the next turn. Since only one pebble is left, WHO$ is the player who just got stuck with the last pebble!
After listing all of the subroutines, the mainline routine is a bit disappointing. It is only six statements.
10 REM ******************************************************** 20 REM * NIM1 * 30 REM * Play the ancient game of NIM * 40 REM ******************************************************** 50 QUANT% = 17 60 GOSUB 800 'Display instructions 70 IF WHO$ = "I" THEN GOSUB 300 ELSE GOSUB 500 80 IF QUANT% = 1 THEN GOTO 1000 90 PRINT QUANT% "items are left." 100 GOTO 70
The mainline routine forms a loop. The only way out is to pass the IF-THEN test on line 80. As you can see, when a flowchart is placed along side of the source code, there is not much more to say. That is the whole purpose of flowcharting.
Creating a user friendly program was important in the design of NIM1. The program has good, clear instructions. It uses the LEFT$ function so the human player can enter just about any reply and still be understood. Even the prevention of cheating can be considered user friendliness. When NIM1 asks for a 1, 2, or 3, by golly, you cannot enter -5 or 32. Well designed programs do as much as possible for the player. Make your programs simple to use. Make them so they cannot be "broken." And when you are finished, go back and make them better. Watch how other people play your games. If players make mistakes, change your program. Use more PRINT statements so the players understand what to do. Add IF-THEN tests to prevent and correct mistakes. Write BASIC code that can take what a player typed and figure out what they meant. For example, in NIM1, the player can enter "nope" when asked "Do you want to go first?" Since NIM1 only looks at the first character, the program "knows" what they really mean.
Write programs as if all humans were bimbos. Put the intelligence into the program and do not depend on the human user of the program. Perhaps your program can ask the player's name. Store this in a variable and then use it occasionally. Make the human feel like the program is truly intelligent.
The term artificial intelligence is often used in modern computing. It is a buzz word that is widely used but seldom defined. Even the experts disagree on definitions. We know what user friendly programs do. They make assumptions. What is intelligence? Some would argue that intelligence is the ability to draw conclusions from incomplete information. Others say this is too simple. Most agree that a program could be considered to have the appearance of intelligence when a user would not be able to tell whether a computer or a human was responding. Is there a difference between intelligence and the appearance of intelligence?
While the experts argue over whether computer programs can really be intelligent, programmers write better programs and engineers create faster machines. Indeed, the question may be answered someday -- by a computer! The appearance of intelligence is more a matter of CPU speed and memory size than it is of anything else. Fast computers can execute large programs in the blink of an eye. The large programs will have all the instructions needed to form opinions, guesses, and assumptions.
No one will claim that a one-page BASIC program is intelligent. However, the appearance of intelligence is a worthy goal no matter how small the program.
One trait of intelligence is the ability to learn. Let's give Nim a little more intelligence. Let's teach it to look for certain numbers and improve its chances of winning. Add these lines to the program.
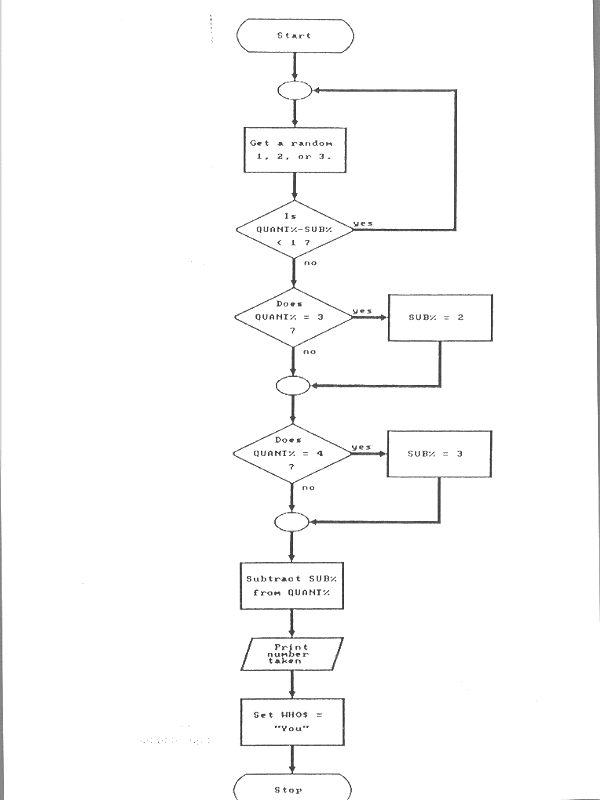
20 REM * NIM2 * 332 IF QUANT% = 3 THEN SUB% = 2 334 IF QUANT% = 4 THEN SUB% = 3
We can see how these lines change Nim's decision-making process by looking at Figure 7 on page 77. After the program randomly selects a 1, 2, or 3, two IF-THEN tests are made. The first checks if QUANT% is equal to 3. If so, then the number in SUB% is changed to 2. The computer wins! A similar action is taken if QUANT% is equal to 4. We have now taught the computer how to win when the number of pebbles is less than five. Indeed, the computer will always win if you let the number of pebbles get down below five. Is there anything more you can "teach" the computer? Why do we not have a test for only two pebbles? Are there any other ways we could change the subroutine? What would happen if the computer copied every move made by the human? Since the program was written with subroutine building blocks we can test some of these questions. Just write a new subroutine. And don't forget the flowchart.
TopChapter 5 [... Table of Contents] Chapter 7