Chapter Eight: Guess Again
In chapter five we matched wits with the computer. Using random number routines, the computer created a secret number. Then we discovered the number using as few guesses as possible. To do this, we used a binary search. Now it is time to turn the tables and make the computer guess our secret number. Of course, this means we must first write a program that knows how to do a binary search.
A binary search, you will recall, is a process of elimination. With every guess we eliminate half of the choices. We always guess the middle number of whatever range is presented. If the secret number is in the range 1 to 100, then we guess 50. This instantly narrows the search by half. Instead of one hundred choices, we now have only fifty. The next guess cuts the range to only twenty-five. A binary search is a quick way to find one number among many.
Now that we can explain in words how to do a binary search, we must turn these words into BASIC statements for the computer. BASIC does not have a binary search command. Instead, we must build a binary search program using ordinary arithmetic. To do this, we need a plan. In computer terms, a plan for solving a problem is called an algorithm. Our binary search algorithm is a step-by-step plan for guessing a number in the middle of a range of numbers. It has to work, not only for 1 through 100, but for any range. The algorithm has three steps:
- Find how many numbers we have from which to choose.
- Divide this range by two.
- Add the quotient to the lower limit (or subtract it from the upper limit).
Now we are getting close to something that can be written in BASIC. Let us define some variables. LOW% is the low end of the range. HIGH% is the upper limit. Both, of course, are integer variables. We can start with these variables and calculate some others. Compare these following three lines of BASIC with our three steps above.
410 RANGE% = HIGH% - LOW% 420 HALFWAY% = RANGE% \ 2 430 MIDDLE% = LOW% + HALFWAY%
Examine line 410. First we subtract LOW% from HIGH%. This results in the number of numbers in the range. Suppose we may have a range of 50. It does not matter if this is from 1 to 50, 25 to 75, or 50 to 100. We just know we have a spread of fifty numbers. In line 420, the range is divided by 2. We will need this number in order to find the middle point in the range. Finally, in line 430, we add HALFWAY% to the lower limit to find the middle number. MIDDLE% will be the computer's guess.
The first line uses the upper and lower limits to calculate RANGE%. The second line calculates HALFWAY% by dividing RANGE% by two. The last line uses the lower limit and HALFWAY% to calculate a guess. The algorithm starts out with just an upper and a lower limit and, with each step, calculates one unknown. Each step builds on the earlier steps.
To see if our algorithm works, let's trying using some real numbers for HIGH% and LOW%. Enter the subroutine and temporarily add some lines which let us see the algorithm working.
10 INPUT "Enter high ",HIGH% 20 INPUT "Enter low ",LOW% 400 REM ****** CALCULATE A GUESS ***** 410 RANGE% = HIGH% - LOW% 420 HALFWAY% = RANGE% \ 2 430 MIDDLE% = LOW% + HALFWAY% 440 PRINT"RANGE% ="RANGE%" HALFWAY% ="HALFWAY%" MIDDLE% =" MIDDLE% 450 GOTO 10
Before running this program, look carefully at line 420. This statement divides the variable RANGE% by 2. The backslash (\) is BASIC's symbol for integer division. When doing integer division, BASIC ignores any fraction that may be left after the division. For example, 13 divided by 2 using integer division is equal to 6. The quotient is NOT rounded! While we may know that 13 divided by 2 equals 6.5, BASIC simply drops the .5 and sets the quotient equal to 6. If better accuracy is needed, use single precision variables and the forward slash (/).
Now RUN this program. Start with a high limit of 100 and a low limit of 0. Then, leave 100 as the high and set low equal to the MIDDLE% that is produced each time through the routine. You program should produce these numbers:
HIGH% LOW% RANGE% HALFWAY% MIDDLE%
100 0 100 50 50
100 50 50 25 75
100 75 25 12 87
100 87 13 6 93
100 93 7 3 96
100 96 4 2 98
100 98 2 1 99
100 99 1 0 99
This test shows us we have a problem. HIGH% and LOW% are input to the algorithm; MIDDLE% is output. It is the guess. If the secret number was 100, our program could not guess it! Look at the last line. When 100 is the high limit and 99 is the low limit, BASIC divides the range of 1 by 2 producing 0.5. Since integer division does not round, HALFWAY% becomes 0. Zero is added to 99. We are stuck at 99. What can we do?
Let us change the high limit. Run this program again using 101 as the high limit and 0 as the low limit.
HIGH% LOW% RANGE% HALFWAY% MIDDLE%
101 0 101 50 50
101 50 51 25 75
101 75 26 13 88
101 88 13 6 94
101 94 7 3 97
101 97 4 2 99
101 99 2 1 100
This time it worked. If 100 was the secret number, our algorithm would find it. Now we must test the routine at the other extreme. Can the program produce a guess of 1? Run the program again. Begin with limits of 101 and 0, but this time keep 0 as the low limit and use the MIDDLE% number as the high limit each time through the routine.
This work has accomplished two things. First, we now know that our binary search routine must begin with limits of 0 and 101 in order to guess a number in the range of 1 through 100. Second, we have used the building block approach to writing programs. The guessing program is still largely undefined. However, the most important subroutine is now fin- ished. This is one of the advantages of writing programs using subroutines. They are easier to plan, since each task can be placed in a separate subroutine, and they are easier to test. Why wait until the whole program is finished? Test each subroutine as it is created.
Once the testing is complete, we can DELETE the BASIC statements that were needed only for testing. Get rid of lines 10, 20, 440, and 450. Here is the finished routine as it will be used in the final program:
400 REM ****** CALCULATE A GUESS ***** 410 RANGE% = HIGH% - LOW% 420 HALFWAY% = RANGE% \ 2 430 MIDDLE% = LOW% + HALFWAY% 440 RETURN
Another important routine prints the instructions to the player. For the binary search routine to work, it must have new high or low limits each time it is executed. The player must reply whether each guess was high, low, or just right. Therefore, we need good instructions.
500 REM ***** DISPLAY INSTRUCTIONS ***** 510 PRINT "*****************************************************" 520 PRINT "* *" 530 PRINT "* Pick a number in the range 1 through 100. *" 540 PRINT "* The computer will guess your secret number. *" 550 PRINT "* Each time the computer makes a guess, you tell if*" 560 PRINT "* the guess is High, Low, or Right On. *" 570 PRINT "* *" 580 PRINT "*****************************************************" 590 RETURN
These instructions seem clear. Each time the computer makes a guess, the human player must reply High, Low, or Right On. However, since we want our program to be user friendly, our program will only require that the first letter of each answer be entered. This task of checking the reply is handled by another subroutine.
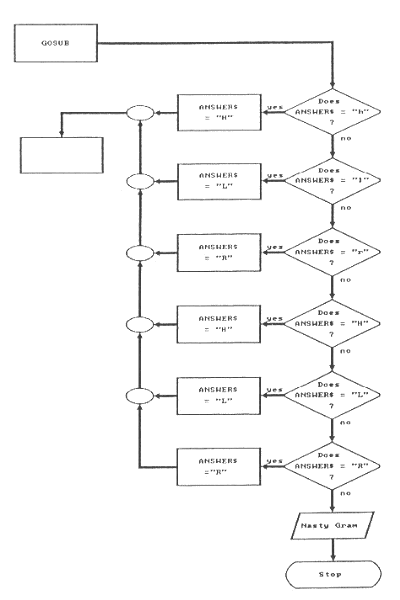
600 REM ***** DECODE THE ANSWER ***** 610 IF LEFT$(ANSWER$,1) = "h" THEN ANSWER$ = "H":RETURN 620 IF LEFT$(ANSWER$,1) = "l" THEN ANSWER$ = "L":RETURN 630 IF LEFT$(ANSWER$,1) = "r" THEN ANSWER$ = "R":RETURN 640 IF LEFT$(ANSWER$,1) = "H" THEN ANSWER$ = "H":RETURN 650 IF LEFT$(ANSWER$,1) = "L" THEN ANSWER$ = "L":RETURN 660 IF LEFT$(ANSWER$,1) = "R" THEN ANSWER$ = "R":RETURN 670 PRINT "Invalid input. Your answer must begin with H, L, or R" 680 END
Parts of this routine should look familiar. The LEFT$ function is used to strip off all but the first letter of the variable ANSWER$. The six IF-THEN statements check for either an upper or lower case H, L, and R. If one of these letters are found, then the ANSWER$ variable is changed to just the single upper case character. Notice that each of the six IF-THEN statements ends with :RETURN. This is new.
A colon in BASIC is used to stack more than one command on a line. In this case, a RETURN statement is added to each of the IF-THEN tests. Look at line 610. If BASIC finds the first character of ANSWER$ to be a lower case H, it changes ANSWER$ into an upper case H, and then executes a RETURN. The RETURN only executes if the IF-THEN test is successfully passed. The RETURN closes the GOSUB and program execution continues back in the mainline routine. Any remaining IF-THEN tests are simply skipped.
The colon is especially helpful with IF-THEN statements. It can also be used on any line to combine any BASIC commands. Do not use the colon too much. A program with many statements all stacked on the same line is hard to understand and difficult to change. As a rule, use only one command on each line.
If the ANSWER$ variable contains anything that does not begin with an H, L, or R, then none of the IF-THEN tests are passed and lines 670 and 680 will be executed. Because of the :RETURN additions, the only way to get to lines 670 and 680 is to enter something that does not begin with H, L, or R. A flowchart makes this clear. See Figure 10 on page 100. Each decision box represents one of the IF-THEN tests.
The last subroutine needed is the victory message.
900 REM ***** THIS IS THE END ***** 910 PRINT "Hurray! I did it." 920 RETURN
This completes the four subroutines. The first is the binary search algorithm which calculates the guess. The second just displays the instructions. A third routine decodes the input from the keyboard. This is the routine which introduced the colon (:) as a way to put more than one statement on a line. Note that this routine does not perform the INPUT. That will be done in the mainline routine. The final routine simply displays the winning message.
Here is the mainline routine:
10 REM ********************************************************* 20 REM * IGUESS1 * 30 REM * The computer will guess your secret number. * 40 REM ********************************************************* 50 CLS 60 HIGH% = 101 70 LOW% = 0 80 GOSUB 500 'DISPLAY INSTRUCTIONS 90 GOSUB 400 'CALCULATE A GUESS 100 PRINT "My guess is " MIDDLE% "Is this High, Low, or Right On?" 110 INPUT ANSWER$ 120 GOSUB 600 'DECODE THE ANSWER
130 IF ANSWER$ = "R" THEN GOSUB 900:END 140 IF ANSWER$ = "H" THEN HIGH% = MIDDLE% 150 IF ANSWER$ = "L" THEN LOW% = MIDDLE% 160 GOTO 90 'TRY ANOTHER GUESS
The high and low limits for the binary search subroutine are defined on lines 60 and 70. These are set to the numbers we discovered during testing. Line 80 is the GOSUB which displays the instructions for the game. The processing loop begins on line 90 and continues through line 160.
Line 90 branches to the binary search subroutine. This happens immediately after the instructions are displayed. The first pass through the routine uses the high and low limits defined on lines 60 and 70. Therefore, the first guess will always be 50. The guess is displayed with line 100. The ANSWER$ variable is set with line 110 and then decoded by the GOSUB on line 120. The next three lines are IF-THEN tests using the output of the decoding subroutine. Note that the ANSWER$ variable has now been reduced to a single letter. It can only be an H, L, or R. If that single let- ter is R, then the first test is passed and the GOSUB 900 executes. The victory message is printed. Line 130 also uses a colon (:) to add an END statement. Take a good look at line 130. When ANSWER$ is R, first the GOSUB is executed. Then, after the RETURN on line 920, control passes back to line 130. The next instruction following the colon is executed. This is the end of the game.
If the guess is not correct, then ANSWER$ will not contain an R. Therefore, one of the other two IF-THEN tests will be passed. If the computer's guess is too high, then line 140 changes the high limit. If the computer's guess is too low, then line 150 changes the low limit. With each guess, half of the possibilities are eliminated. Line 90 then branches back to the beginning of the processing loop and another binary search is tried. By this time, either HIGH% or LOW% has been changed in either line 140 or 150. The binary search algorithm uses the new limit to try another guess.
Now that all the BASIC statements have been entered, testing must begin. Run the program and make sure that it can guess both 1 and 100. Then try many other numbers. Complete testing demands that we let our program guess all one hundred possibilities! Testing is an important part of pro- gramming. Make sure the program works correctly before you let friends play. You may need to add PRINT statements in several places to see what is happening. These can be used to find problems. These extra PRINTs may be removed later.
Now that we have a working program it is time to think about improvements! A few should be obvious. Color could be added easily. Also, the program can be used to explore binary searches if we count the number of guesses the computer requires to discover a secret number. Then it would be easy to find which numbers are hard to guess using our binary search algorithm. You may also have noticed that the program makes its first guess, always 50, at the same time the instructions are displayed. The guess appears before a player has time to read how to play the game! Perhaps a way could be found to stall. Maybe the program could ask: "Press enter when you are ready to begin." Another subroutine could take care of this task. A GOSUB at line 85 could be added to the mainline routine.
The victory message is rather plain. We could go wild here. Perhaps the subroutine beginning at line 900 could switch to graphics mode, clear the screen, and really get fancy. Maybe even some music could be added. A random number routine could select from two or three tunes. The possibilities are endless!
Be sure to play the UGUESS program from chapter five and then use those secret numbers with IGUESS. Who is better at guessing, you or the computer?
TopChapter 7 [... Table of Contents] Chapter 9